Differentiable Modeling of Percussive Audio with Transient and Spectral Synthesis

Jordie Shier, Franco Caspe, Andrew Robertson, Mark Sandler, Charalampos Saitis, and Andrew McPherson


Code | Paper


Abstract

Differentiable digital signal processing (DDSP) techniques, including methods for audio synthesis, have gained attention in recent years and lend themselves to interpretability in the parameter space. However, current differentiable synthesis methods have not explicitly sought to model the transient portion of signals, which is important for percussive sounds. In this work, we present a unified synthesis framework aiming to address transient generation and percussive synthesis within a DDSP framework. To this end, we propose a model for percussive synthesis that builds on sinusoidal modeling synthesis and incorporates a modulated temporal convolutional network for transient generation. We use a modified sinusoidal peak picking algorithm to generate time-varying non-harmonic sinusoids and pair it with differentiable noise and transient encoders that are jointly trained to reconstruct drumset sounds. We compute a set of reconstruction metrics using a large dataset of acoustic and electronic percussion samples that show that our method leads to improved onset signal reconstruction for membranophone percussion instruments.


Audio Results

Here we share resynthesis results from our method on a selection of acoustic and electronic drum set sounds from our test set. \(Y\) is the ground truth audio target, \(S\) is sinudoial only using sinusoidal modeling, \(S + N\) is sines plus noise with a learned noise encoder and generator, and \(T(S) + N\) uses the learned transient encoder and modulated TCN network conditioned with a sinusoidal input and noise is summed at the ouput.

Target \(Y\) \(S\) \(S + N\) \(T(S) + N\)
Acoustic Kick
Acoustic Snare
Acoustic Tom
Acoustic Hihat
Acoustic Crash
Electronic Kick
Electronic Snare
Electronic Tom
Electronic Hihat
Electronic Crash


Spectral Flux Reconstruction

To evaluate transient reconstruction we used the \(L_2\) error between spectral flux onset envelopes, which are commonly used for onset detection. We present a couple examples here to provide more insight into how the transient TCN network impacts this metric.

First, here is a snare drum example where the transient network clearly improves the spectral flux over using sinusoids and sinusoids plus noise only.

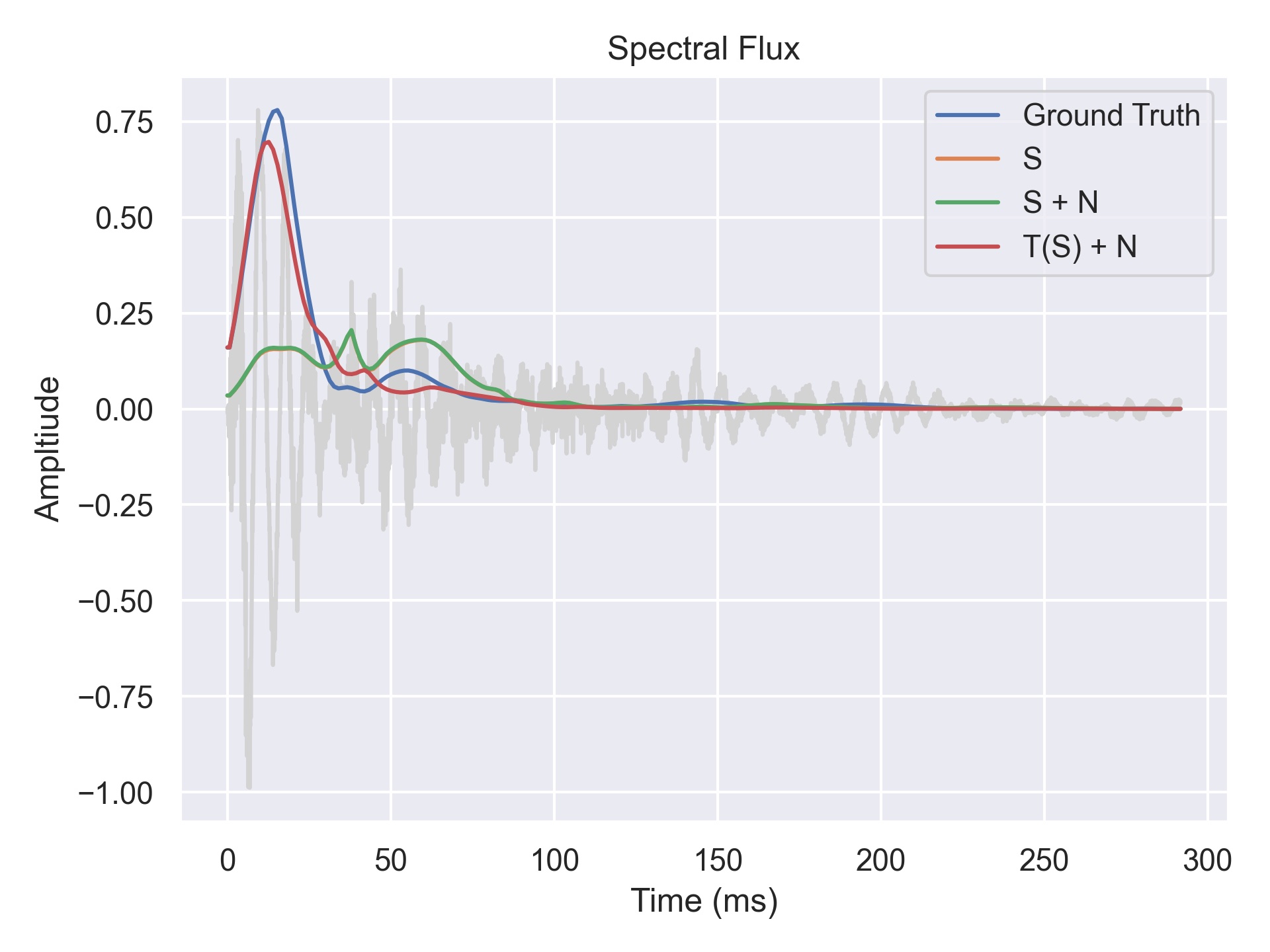
Audio files containing the original (ground truth) followed shortly by a reconstruction:

\(S + N\)
\(T(S) + N\)


Which version do you think has a better transient?


Now, here is a counter example of a hihat where the transient network does not improve the spectral flux onset metric.

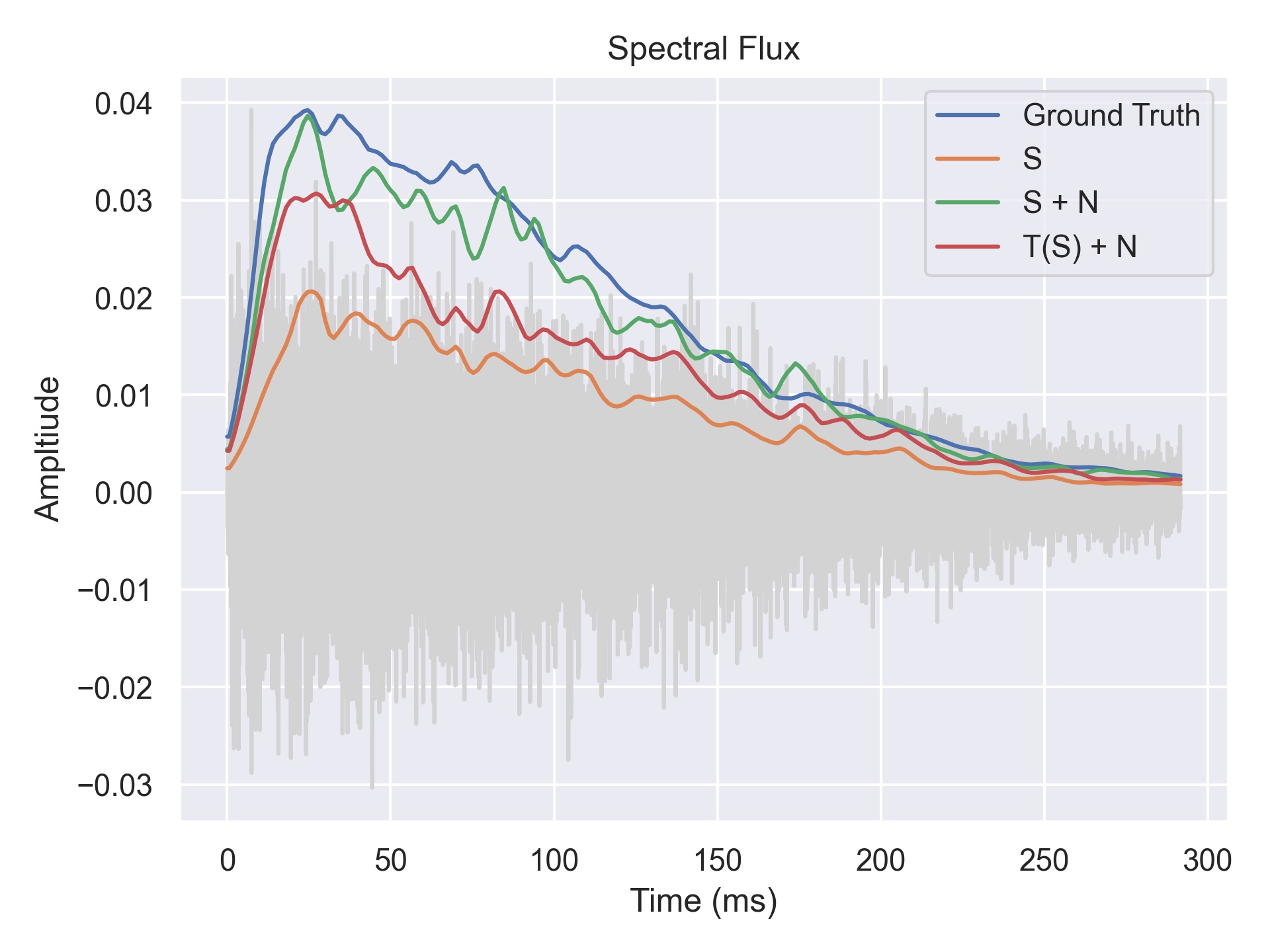
Audio files containing the original (ground truth) followed shortly by a reconstruction. We can also hear artefacts in the noise reconstruction – potentially attempting to make up for a lack of higher harmonics in the sinusoidal modelling.

\(S + N\)
\(T(S) + N\)


Transient TCN Configuration

Our transient reconstruction temporal convolution network (TCN) \(T()\) is based on the TCN by Christian Steinmetz and Joshua Reiss for modelling the LA2A compressor [1]. However, we use an increasing dilation rate of factor two instead of ten as we aren’t as interested in modeling long-term temporal dependecies. The details of the model are outlined in the figure below.

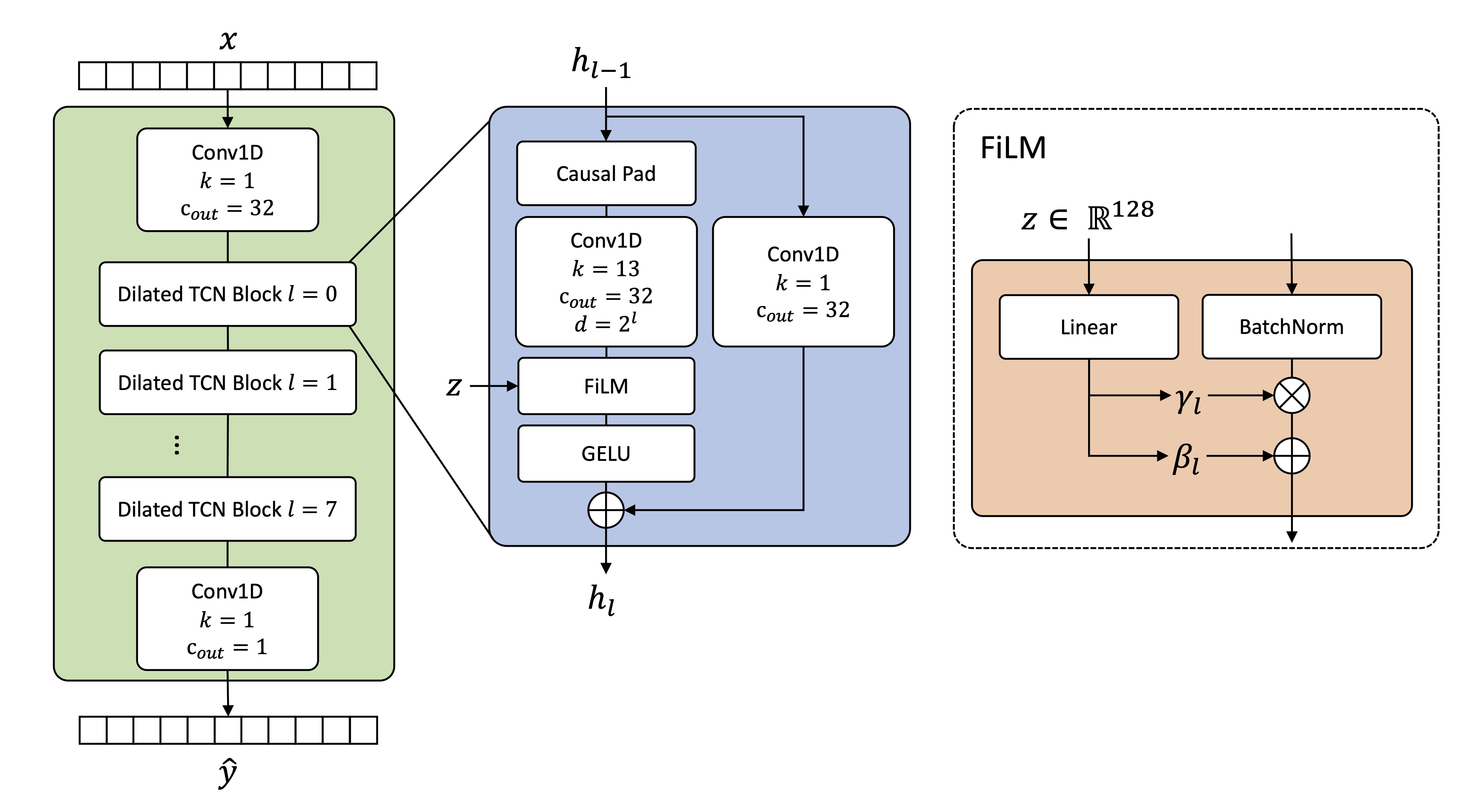
The input to the TCN is an audio waveform \(x\). An input projection layer maps this input to 32 output channels \(c_{out}\). All intermediate TCN operations use 32 hidden channels. There are 8 dilated TCN blocks (i.e., 8 layers). Each dilated TCN block comprises a causal pad which ensures the output \(h_{l}\) of the convolution at the current layer has the same length as the input to that layer \(h_{l-1}\). The main temporal convolution at each layer uses a kernel size of \(k=13\) and a dilation equal to \(2^l\) where \(l\) is the layer number. The output is modulated via an affine transform in a feature-wise linear modulation (FiLM) [2] block. Scale and shift parameters for the affine transformation are learned independently for each layer \(l\) using a linear projection. A gaussian error linear unit (GELU) acivation is applied before mixing with the residual. Finally, an output projection convolutional layer maps back to a single channel, the ouput of which is \(\hat{y}\).


Speed Tests

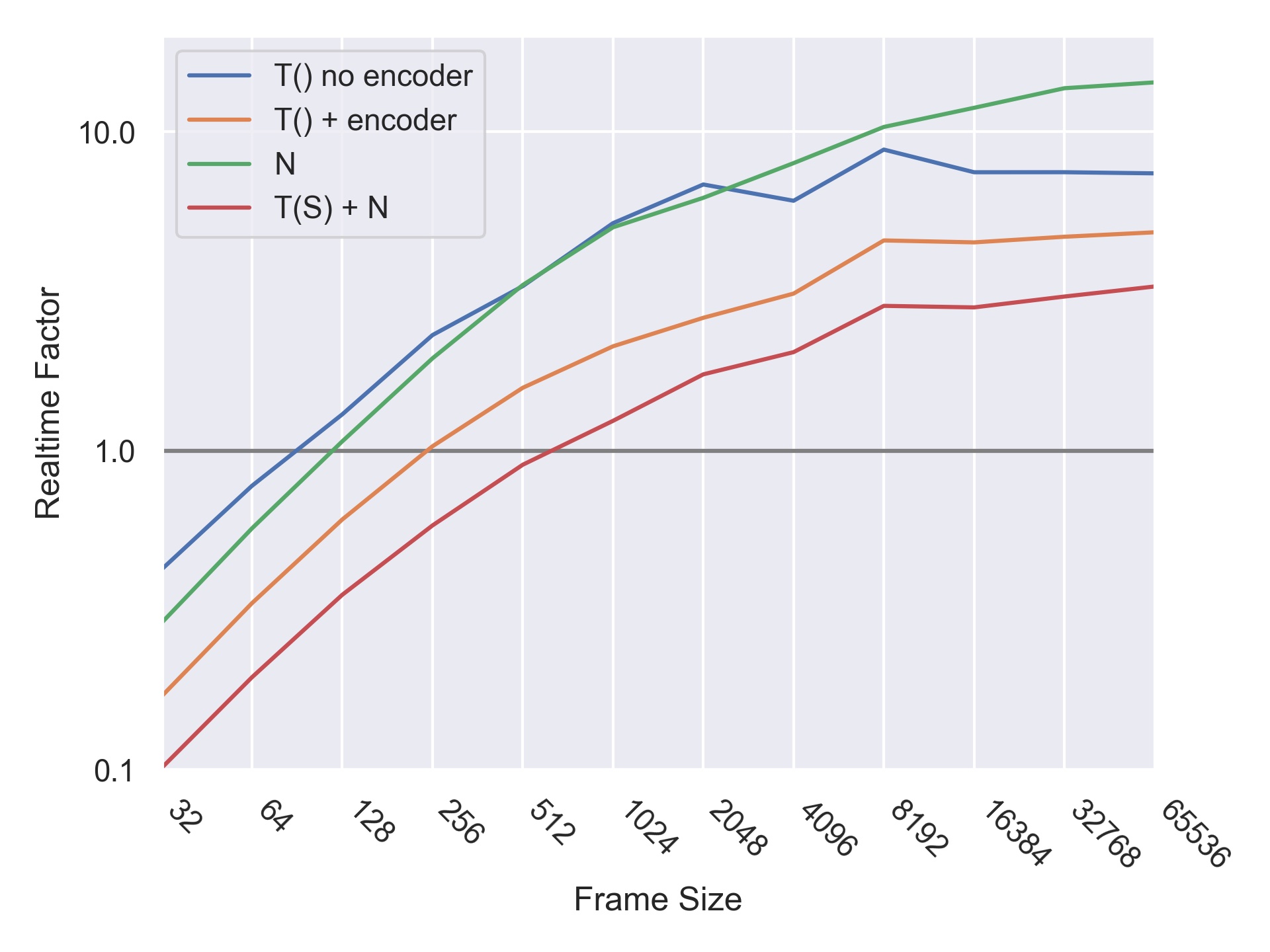
To evaluate the computational efficiency of our synthesis method we tested the rendering speed of various components using different frame sizes. While achieving real-time performance was not a goal of this work, future work includes investigating how these components might be incorporated into a real-time performance system.

Four configurations of the model were tested: 1) The transient TCN \(T()\) without the transient encoder stage; 2) the transient TCN preceded by the transient encoder, which produces the latent transient embedding used for FiLM; 3) the noise synthesizer with the noise encoder; 4) the full model with all the encoders and sinusoidal synthesis. Since CQT sinusoidal modeling synthesis is a preprocessing step and is not causal, we do not include it in these calculations.

Realtime factor is calculated as the frame size in seconds at a sampling rate of 48kHz divided by the time required to compute that frame size. A frame size greater than 1 is required for real time processing.

Computed on an Apple M1 Pro (cpu-only).


References

[1] Steinmetz, Christian J., and Joshua D. Reiss. “Efficient neural networks for real-time modeling of analog dynamic range compression.” arXiv preprint arXiv:2102.06200 (2021).

[2] Perez, Ethan, et al. “Film: Visual reasoning with a general conditioning layer.” Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 32. No. 1. 2018.