Real-time Timbre Remapping with Differentiable DSP

Jordie Shier, Charalampos Saitis, Andrew Robertson, and Andrew McPherson

Training Code | Audio Plugin (Coming Soon!) | Paper

Abstract

Timbre is a primary mode of expression in diverse musical contexts. However, prevalent audio-driven synthesis methods predominantly rely on pitch and loudness envelopes, effectively flattening timbral expression from the input. Our approach draws on the concept of timbre analogies and investigates how timbral expression from an input signal can be mapped onto controls for a synthesizer. Leveraging differentiable digital signal processing, our method facilitates direct optimization of synthesizer parameters through a novel feature difference loss. This loss function, designed to learn relative timbral differences between musical events, prioritizes the subtleties of graded timbre modulations within phrases, allowing for meaningful translations in a timbre space. Using snare drum performances as a case study, where timbral expression is central, we demonstrate real-time timbre remapping from acoustic snare drums to a differentiable synthesizer modeled after the Roland TR-808.

Presentation

Demos

These demos were recorded with professional drummer Carson Gant using a prototype audio plug-in. All models used in these videos were trained on short (~1min) recordings of Carson playing and all recordings were created in real-time.

Short Overview Demo

Short performance passages followed by the synthesized version. A few different synthesizer presets are included for demonstration.

Longer Performance Demos

Two videos of the same performance are shown for each model and corresponding synth preset: one with only the synthesized audio and one with the original drum sound mixed in.

Snare Preset 1

Synth Only Mix:

Synth plus Drum Mix:

Snare Preset 2

Synth Only Mix:

Synth plus Drum Mix:

Snare Preset 3

Synth Only Mix:

Synth plus Drum Mix:

Snare Preset 1 - Missed Hits

Example of playing from quiet to loud, showing that quiet hits were not captured well with this particular onset detection setup. Cresendos on the drumhead show more dynamic range than the rim hits during synthesis.

Synth Only Mix:

Synth plus Drum Mix:

Model and Training Details

We conducted a series of numerical experiments to evaluate the performance of our differentiable timbre remapping approach. This involved training neural network mapping models to estimate synthesizer parameter modulations to match audio feature differences observed between snare drum hits in a performance. This section supplements the material in the paper with model and training details. Please refer to section 5 in the paper for full details and results.

Mapping Models

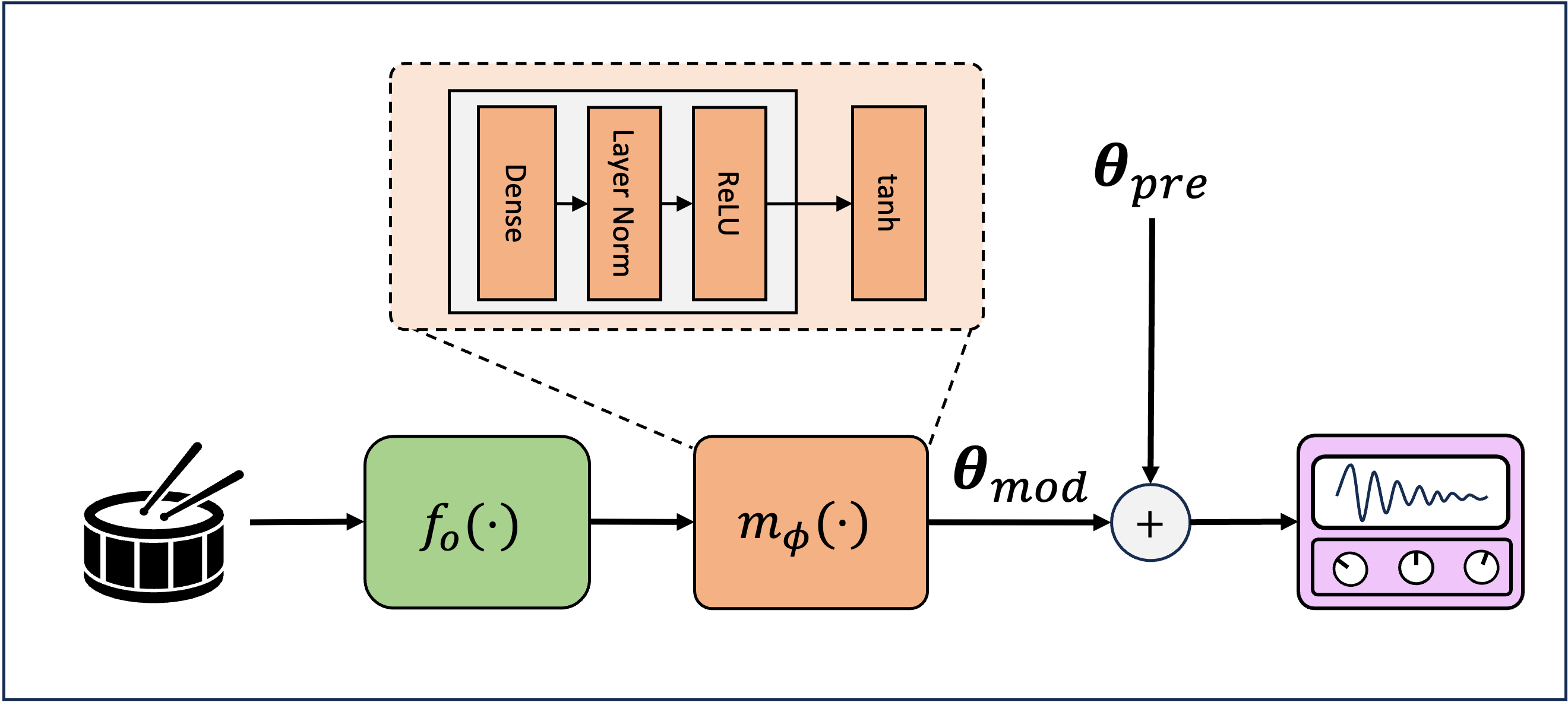
This diagram shows an overview of the multi-layer perceptron (MLP) model used to map onset features to synthesizer parameter modulations. \(f_0(\cdot)\) extracts features from a short window of audio at a detected onset. The result is a feature vector with three dimensions (model input size). \(m_{\phi}(\cdot)\) is a neural network which is trained to estimate synthesizer parameter modulations \(\theta_{mod}\), which is summed with a synthesizer preset \(\theta_{pre}\). \(\theta_{pre}\) is selected prior to training and fixed. The number of synthesizer parameters is 14. Therefore, a mapping model maps from three input features to 14 output parameters.

During numerical experiments we included a baseline linear layer for comparison. The linear model did not include layer normalization. Details of the different architectures are provided in the table below.

Model	Hidden Size	Num Layers	Num Params	Activation	Output
Linear	n/a	0	42	Linear	Clamp (-1.0,1.0)
MLP	32	1	590	ReLU	Tanh
MLP Lrg	64	3	9500	ReLU	Tanh

Training Hyperparameters

Model parameters were initialized by sampling from a normal distribution with zero mean and a standard deviation selected via hyperparameter tuning. All models were trained using an Adam optimizer for 250 epochs. The learning rate was scheduled to decrease by a factor of 0.5 when a validation loss plateaud for 20 epochs. Initial learning rates are shown in the table below.

Model	Weight Initialization Std	Learning Rate
Linear	1e-6	5e-3
MLP	1e-3	5e-4
MLP LRG	1e-3	5e-4

Direct Optimization

For numerical experiments we compared against results obtained by directly optimizing synthesizer modulation values. No models were trained. The synthesizer modulation values were treated as learned parameters and directly optimized for each drum sound in a dataset. This represents an upper-bound for mapping model performance. For this we used an Adam optimizer with a learning rate of 5e-3 which was scheduled to decrease by a factor of 0.5 after 50 iterations with no decrease in loss. Parameters were optimized for 1000 iterations.